Operative Terminplanung steigert die Effizienz in der Produktion

Anbieter zum Thema

Hermann Kemper GmbH & Co. KG - Hersteller für CNC Drehteile

Fastems Systems GmbH

SCIO Automation GmbH

STOHRER Surface AG

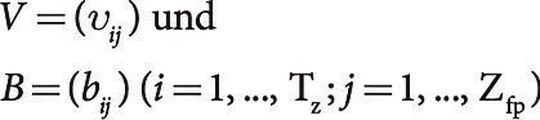
Mathematisch werden für diese Aufgabe zwei Matrizen benötigt, in die die Ausgangsdaten eingegeben werden.

Dabei ist υij die nummerierte Reihenfolge der Teile einer Losgröße mit der i-ten Bezeichnung am j–ten Arbeitsplatz.

Nun muss eine Maschinenbelegung gefunden werden

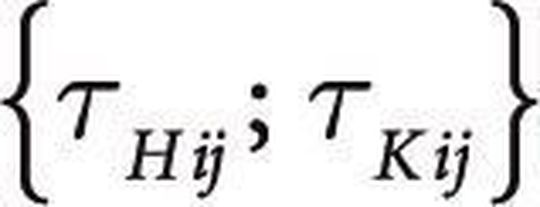
bei der folgende Bedingungen erfüllt sind:

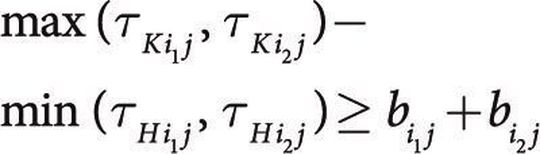
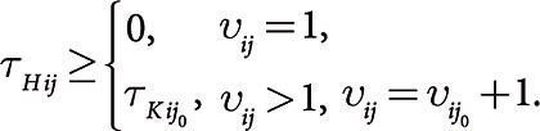
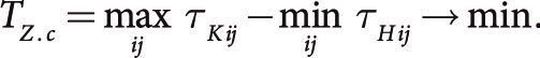
Bedingung (3) zeigt, dass auf der j-ten Maschine keine zwei Teile i1 und i2 gleichzeitig zur Bearbeitung eingeplant werden können. Aus Bedingung (4) folgt, dass mit der Bearbeitung der Teile mit i-ten Bezeichnung aus einem Los auf dem j-ten Arbeitsplatz nicht begonnen werden darf, bevor die Bearbeitung der Teile auf dem j0-ten Arbeitsplatz vollendet ist. Aus Bedingung (5) ergibt sich der optimale Terminplan.

Dieses Berechnungsschema stellt den (TZq-1)-Schrittprozess dar, TZ steht dabei für Teilezahl. Im ersten Schritt wird die Matrix

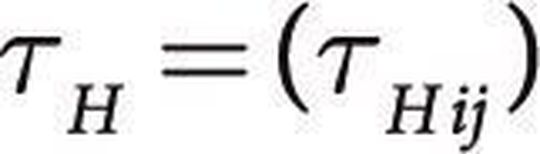
aufgebaut, bei der

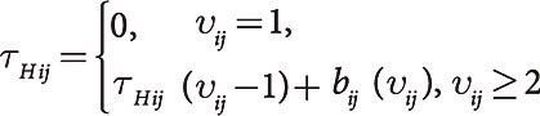
erfüllt sein muss. Somit erfüllt der Kalenderplan Bedingung (4).

Wenn die Größen τ? ij und τ? ij die Bedingung (3) erfüllen, dann bestimmen die Matrixelemente τ den optimalen Fertigungszeitpunkt der Arbeitsplätze, weil die Teilelose ununterbrochen bearbeitet werden und jeder einzelne Arbeitsschritt zum optimalen Zeitpunkt innerhalb der betrachteten Periode beginnt.

(ID:347346)