Dämpfungsmodelle für hochdrehende Spindellager

Anbieter zum Thema

Renishaw GmbH

JESSBERGER GmbH

All for One Group SE

Werkzeugmaschinenlabor WZL RWTH Aachen

Werkzeugmaschinenlabor WZL der RWTH Aachen

Experimentelle Bestimmung von modalen Dämpfungsparametern

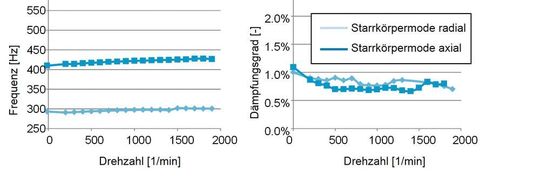
Zur Bestimmung von Dämpfungskennwerten wird der Prüfstand dynamisch vermessen. Es erfolgt eine impuls- oder gleitsinusförmige Erregung der Welle beziehungsweise des Prüfstands. Anhand der Schwingungsantwort des mechanischen Systems kann an den Resonanzstellen die modale Dämpfung ausgewertet werden. Als modale Größe bezieht sie sich allein auf die ihr zugehörige Eigenfrequenz und bildet alle diese Eigenfrequenz beeinflussenden Dämpfungseinflüsse des Systems ab. Somit ist sie allgemein formuliert ein Maß für den Einfluss der Systemdämpfung auf die jeweilige Eigenmode. Ein Rückschluss auf die Dämpfung des Wälzlagers kann nur gezogen werden, wenn die zugehörige Eigenmode beziehungsweise der Eigenvektor eine dominante Relativbewegung zwischen Welle und Lagerbock beschreibt. Zusätzlich dazu sollte das System ein ausgeprägtes Einmassenschwingerverhalten aufzeigen. Bei einem physikalischen System ist ein solches Verhalten dadurch gekennzeichnet, dass die Resonanzüberhöhungen sich nur sehr schwach gegenseitig beeinflussen. Für die Untersuchungen der Lagereigenschaften sind nur die Starrkörpermoden von Belang, weil diese hauptsächlich von den Lagersteifigkeiten- und Dämpfungen beeinflusst werden und ermöglichen, jeweils nur eine Raumrichtung isoliert zu betrachten. Bild 3 zeigt die Ergebnisse der Versuche im Stillstand für die relevanten Starrkörpermoden, die im Folgenden nach ihrer Bewegungsart (Radiale Auslenkung, Axiale Auslenkung und Kipp- Drehbewegung) benannt werden, wobei für die Radial- und die Kippbewegung jeweils zwei Bewegungsebenen zusammenfasst werden.

Der Einfluss der Vorspannung ist deutlich ersichtlich. Eine ansteigende Vorspannung hat ein abnehmendes Dämpfungsmaß zur Folge. Weiterhin ist zu erkennen, dass die Kippmode tendenziell die geringste Dämpfung aufweist, die Radialmode die höchste. Das in dem untersuchten Zustand keine hydrodynamischen Schmierbedingungen im Kontakt vorherrschen, führt dazu, dass keine Aussage über das Dämpfungsverhalten im Betrieb getroffen werden kann. Dadurch sind weitere Untersuchungen notwendig.

Theoretische Berechnung von Lagergrößen

Die physikalische Dämpfung im Gesamtlager setzt sich aus der Dämpfung der einzelnen Kontaktstellen im Wälzkontakt zusammen. Daher ist es für eine Modellableitung wichtig, Kenntnis über vorherrschende Bedingungen in den Wälzkontaktstellen zu haben. Da diese Größen nur schwierig zu messen sind, muss sich theoretischer Modellvorstellungen oder umfangreicher und mit großem Aufwand erhobener experimenteller Daten bedient werden. Die Größen, die von Bedeutung sind, sind unter anderem die Kontaktpressung sowie die Schmierfilmhöhe, wobei letztere zunächst nicht betrachtet werden soll. Für die Kontaktpressungen sollen die Annahmen für Hertz’sche Punktkontakte übernommen werden, auch wenn strenggenommen ein elasto-hydrodynamischer Kontakt vorliegt. Untersuchungen haben jedoch ergeben, dass der Hertz’sche Kontakt eine in Teilen und abhängig von den Betriebsbedingungen gute Näherung des EHD-Kontaktes darstellt. Insbesondere gilt dies für hochbelastete Punktkontakte, deren Annahmen bei höheren Drehzahlen gerechtfertigt sind [6]. Die Schmierfilmparameter sollen später mittels empirisch abgesicherter Näherungsgleichungen, wie sie zum Beispiel in [6] benannt sind, bestimmt werden.

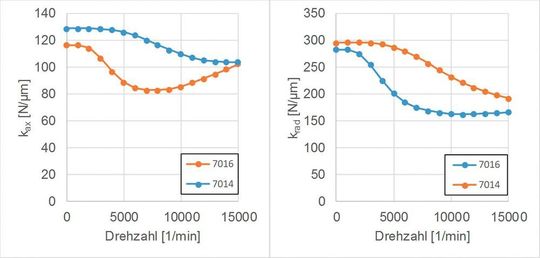
Nach Bestimmung der sich ändernden Lagergrößen, können diese mit der Änderung der Dämpfung im Betrieb korreliert werden. Durch diese Korrelation besteht die Möglichkeit, im Nachgang ein Dämpfungsmodell abzuleiten. Bild 4 zeigt beispielhaft berechnete Lagersteifigkeiten der Baugrößen 7016 und 7014 in Abhängigkeit der Drehzahl. Es ist zu erkennen, dass sich die Steifigkeit z.T. erheblich ändert, wodurch das gesamte dynamische System verstimmt wird.

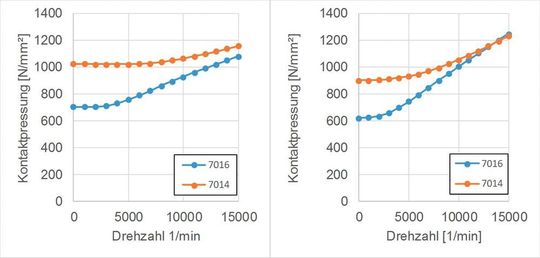
Weiterhin zeigt Bild 5 den Einfluss der Drehzahl auf die Kontaktpressungen in den Wälzkontakten der einzelnen Lager. Da keine externen Lasten an den Lagern anliegen, sind alle Punktkontakte gleich belastet. Es zeigt sich auch hier ein starker Einfluss der Drehzahl auf die Kontaktpressungen, woraus wiederum eine Änderung der Schmierbedingungen resultiert. Dies hat auch Auswirkungen auf das Dämpfungsverhalten der Wälzkontakte.

Erste Versuche zur Untersuchung des Drehzahleinflusses haben gezeigt, dass sich die Dämpfung im unteren Drehzahlbereich nur marginal verändert. Grundsätzlich ist jedoch davon auszugehen, dass sich dies bei höheren Drehzahlen ändert, da sich die Wälzkontakte im Vergleich zum niedrigen Drehzahlbereich ebenfalls stark verändern, wie auch die Berechnung in Bild 5 zeigt. In weiteren Experimenten soll diese Hypothese genauer untersucht werden.

Modellabgleich und Ableitung von physikalischen Dämpfungsparametern

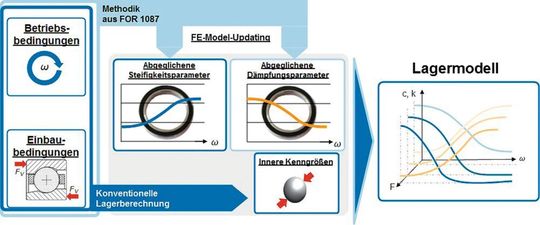
Für den Rückschluss von der gemessenen modalen Dämpfung auf die physikalische Dämpfung wird das Prinzip des FEM-Model-Updating verwendet, mit dessen Hilfe ein FEM Simulationsmodell so angepasst wird, dass es zu den experimentell erhobenen Daten passt. Die Lagerdämpfung wird für den Abgleich zunächst als viskos angenommen. Über einen iterativen Prozess wird das Berechnungsmodell solange angepasst, bis die Zielfunktionen, hier die modalen Parameter, von Modell und Messung möglichst gut übereinstimmen. Die Einordnung des FE-Updatings in den Gesamtkontext der Untersuchungen ist in Bild 7 zu sehen. Die berechneten physikalischen Lagerparameter werden als abgeglichene Steifigkeits- beziehungsweise Dämpfungsparameter genutzt, um durch eine Korrelation mit den berechneten, inneren Lagerkenngrößen aus der iterativen, konventionellen Lagerberechnung ein Lagermodell basierende auf experimentellen und simulativen Eingangsdaten zu entwickeln.

Modellvalidierung an industriell eingesetzten Spindelsystemen

Eine Validierung der gewonnenen Dämpfungsmodelle erfolgt an industriell eingesetzten Spindelsystemen, die von den Projektpartnern eigens für die Dämpfungsuntersuchungen zur Verfügung gestellt werden. Validiert wird über den gesamten verfügbaren Drehzahlbereich des jeweiligen Systems. Hierzu werden die im Lagerprüfstand vermessenen Lager in ein Spindelsystem eingebaut und dynamisch, mithilfe von Nachgiebigkeitsfrequenzgängen, vermessen. Zum Abgleich wird ein der Spindel nachempfundenes FE-Modell genutzt, um das abgeleitete Lagermodell zu implementieren und einen Vergleich mit den experimentell ermittelten Nachgiebigkeitsfrequenzgängen ziehen zu können. Die Übereinstimmung zwischen Modell und Messungen ist somit ein Maß für die Güte des Lagermodells und soll für verschiedene Lagerungen und Drehzahlbereiche überprüft werden.

Nach der Validierung des Lagermodells besteht die Möglichkeit das Dämpfungsmodell um weitere Einflussparameter zu erweitern. Hierzu zählen Schmierstoffparameter, wie die Viskosität. Eine weitere mögliche Erweiterung ist die Anpassung der Berechnung der inneren Lagerkenngrößen, indem nicht mehr vom Hertz’schen Kontakt ausgegangen wird, sondern die Strömungsverhältnisse im Wälzkontakt, über die direkte Berechnung des EHD-Kontaktes, berücksichtig werden. Hierdurch können Wälzkörperverformung inklusive Schmierfilmeinfluss berücksichtigt werden.

Literaturverzeichnis

[1] Brecher, C.; Fey, M.; Wagner, M.: Dämpfung in Profilschienenführungen. wt Werkstattstechnik Online, 2014, Nr. 104. S. 295-300.

[2] Brecher, C.; Fey, M.; Habermann, R.: Comparison of damping properties of spindle bearings. The 16th International Conference on Machine Design and Production, 2014.

[3] Brecher, C.; Habermann, R.; Fey, M.: Dämpfung von Loslagerkomponenten einer Hauptspindel. ZWF – Zeitschrift für wirtschaftlichen Fabrikbetrieb, 2015, Nr. 03.

[4] Brecher, C.; Habermann, R.; Fey, M.: Modeling of the contact damping in tool interfaces. Practical Aspects of Structural Dynamics – Vibrations, Damping. Bernau am Chiemsee: NAFEMS, 2015. S. 46-53.

[5] Brecher, C.; Habermann, R., Motschke, T.; Bergs, C.: Dämpfungseigenschaften der SK 40-Schnittstelle. S I/2016, 2016. S. 40-43.

[6] Harris, T. A.; Kotzalas, M. N.: Advanced Concepts of Bearing Technology. Fifth Edition. 5. Aufl. Boca Raton, Florida: CRC Press, 2007.

Dämpfung in Maschinenkomponenten

Komponentendämpfung im Kontext der Werkzeugmaschine

(ID:44946796)