Hochbelastete CFK-Strukturteile kosteneffizient im Spritzguss fertigen

Anbieter zum Thema

Fachhochschule Osnabrück

PFLITSCH GmbH & Co. KG

ACE Stoßdämpfer GmbH

Renishaw GmbH

Rotationssymmetrie reduziert geometrische Schwachstellen

Um bei der Entwicklung dieses Demonstratorbauteils geometrische Schwachstellen durch beispielsweise Asymmetrien zu minimieren, wurde eine rotationssymmetrische Geometrie gewählt. Die finale Struktur ist hierbei durch eine Kombination aus Topologie- und Wanddickenoptimierungen sowie intelligenter Konstruktion entwickelt worden. Um die Steifigkeit und Festigkeit des Bauteils zu bewerten, können direkte Kenngrößen aus dem Zugversuch in der Simulation nur bedingt verwendet werden, da sowohl kurz- als auch langfaserverstärkte Kunststoffe verarbeitungsbedingt anisotrope und inhomogene Materialeigenschaften aufweisen.

Diese prozessbedingten Einflüsse auf die lokalen Materialeigenschaften wie Faserorientierung, Faserlänge oder Faserkonzentration können bei Struktursimulationen durch die sogenannte „Integrative Simulation“ berücksichtigt werden. [11]

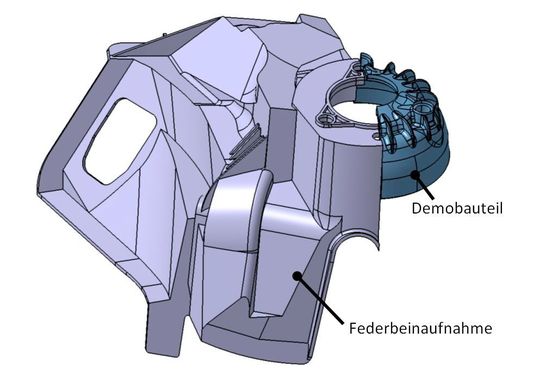
Integrative Simulation mit anisotropem Materialverhalten

Durch steigende Erwartungen an die Prognosegüte von strukturmechanischen Berechnungen reicht es oftmals nicht mehr aus, faserverstärkte Bauteile mit „verschmierten“ Materialansätzen zu berechnen. Bei diesen Ansätzen wird das anisotrope Materialverhalten durch ein isotropes Materialmodell beschrieben, bei denen die Eigenschaften längs und quer zur Spritzrichtung gemittelt werden [12]. Um den Anforderungen gerecht zu werden und Bauteile materialeffizient zu gestalten, muss die Anisotropie in der Struktursimulation berücksichtigt werden. Diese richtungsabhängigen Eigenschaften von kurz- und langfaserverstärkten Kunststoffen, die im Spritzgießprozess verarbeitet werden, ergeben sich durch die Strömungsgegebenheiten im Werkzeug.

Mehr Wissen dank Spritzgießsimulation

Die Faserorientierung kann in der Spritzgießsimulation berechnet und anschließend durch sogenanntes Mapping in die Struktursimulation übertragen werden.

Beim Mapping werden Daten zwischen verschiedenen FE-Netzen, die sich in der Vernetzungsart (Volumenelemente, Schalenelemente, Hybridnetze), der lokalen Diskretisierung und oftmals auch in der Orientierung im Raum unterscheiden, übertragen [11].

Mit Informationen über die vorliegende Faserorientierung kann das anisotrope Materialverhalten in der Struktursimulation berücksichtigt werden. Im Rahmen dieser Untersuchungen erfolgt die anisotrope Materialmodellierung durch die sogenannte „Mean-Field-Theorie“ [13], bei der das nichtlineare Materialverhalten des Verbundes durch Homogenisierungen auf Mikrostrukturebene berechnet wird [11]. Die Basis dieser Homogenisierung bilden die Materialmodelle von Faser und Matrix.

Um hierbei das elastoplastische Materialverhalten der Matrix berücksichtigen zu können, wird deren Spannungs-Dehnungs-Verhalten durch einen linear-elastischen und einen elastoplastischen Anteil beschrieben. Das mechanische Verhalten der Faser wird durch ein isotropes linearelastisches Materialmodell ausreichend berücksichtigt. Die anisotrope Festigkeitsbewertung erfolgt durch die Anwendung eines dehnungsbasierten Tsai-Hill-Kriteriums [14, 15]

(ID:46664629)